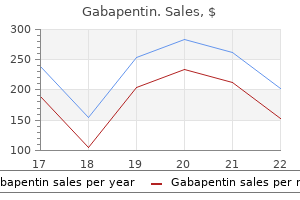
"Buy discount gabapentin 300 mg online, medicine 6 times a day".

S. Runak, M.B.A., M.B.B.S., M.H.S.

Co-Director, Tulane University School of Medicine

Acute exercise increases insulin sensitivity and insulin suppresses lipolysis, therefore it may be used to normalize lipolytic responses to food intake. Microdialysis probes were inserted into the subcutaneous abdominal adipose tissue to monitor interstitial glycerol (lipolysis). Changes in interstitial glycerol concentrations were calculated from one-hour dialysate samples collected before and after ingestion of each meal. There was a poor suppression of lipolysis in abdominal adipose tissue in obese children in response to breakfast that was normalized at lunch, possibly due to the intervening aerobic exercise. Conclusion: the suppressive effect of food intake on lipolysis in subcutaneous abdominal adipose tissue in children may be attenuated after lunch compared to breakfast. The antilipolytic response to food intake can be enhanced with acute exercise in obese children. Our novel data extended our understanding of lipolytic profiles in lean and obese children, thereby providing additional evidence on the role of exercise in treating childhood obesity. Crosssectional data were collected between April ­ October 2014 using a web-based platform. Of the 693, over 90% returned the physical activity monitor and 80% completed all surveys and returned their monitor. Additional links to geospatial data and other policy databases offer multiple research opportunities. Few studies have examined shape/weight valuation (influence of body shape/weight on self-evaluation) as it relates to desire to lose weight among emerging adults, despite the potential to influence weight-related behaviors. Two items from the Eating Disorder Examination assessed weight/ shape valuation: "Over the past 4 weeks, has your shape [weight] influenced how you feel about yourself as a person? Weight dissatisfaction was based on the difference between self-reported weight and goal weight (categorized as desire to lose, stay the same, or gain weight). A chi-square test examined associations between gender and weight dissatisfaction. Logistic regressions explored how shape/weight overvaluation impacted weight dissatisfaction. Results: Significantly more females (76%) than males (41%) reported a desire to lose weight and more males (55%) than females (18%) reported a desire to gain weight (X2(2)=40. Given studies supporting shape/weight overvaluation as a risk factor for maladaptive eating behaviors. The burden of obesity disproportionately impacts African Americans, whose prevalence is significantly higher compared to other ethnic groups. In addition, more than half of African-American women are overweight or obese, which increases the risk for obesity-associated burden and disease. This study evaluated the influence of obesity measures on physiological and cognitive variability in young adult African-American women. The relationship among these variables, and, central cognitive mechanisms associated with the dorsolateral prefrontal cortex and right hemispheric set shifting are discussed. In addition, further discussions on the significance of observable cerebral patterns before a chronic condition diagnosis were explained. Indeed, the holistic Health at Every Size paradigm emphasizing body appreciation and intuitive eating is receiving increased scholarly attention within this literature. Yet research remains to be guided by a cohesive model predicting cardiometabolic health outcomes that also incorporates the potential intermediary roles of stress experienced at this juncture. Structural equation modeling was used to test a model integrating both known relationships among body appreciation, intuitive eating and cardiometabolic outcomes, while assessing the unique impact of stress on both positive and negative eating behaviors. Results indicate a strong model fit along with strong regression coefficients significant (p <. As expected, body appreciation at matriculation had a positive effect on intuitive eating. In turn intuitive eating at matriculation predicted a healthier cardiometabolic profile later in the academic year, but stress (both college-related stress and sexism-related stress) disrupted intuitive eating behaviors. How findings may help inform the development of holistic health promotion efforts for first-year college women are discussed. However, explorations of the relationship between emotional eating and outcomes after bariatric surgery are less conclusive, with some studies suggesting emotional eating is a potent predictor of weight loss after surgery, while others indicate that emotional eating has little impact on post-surgery weight loss. Additionally, research examining the link between emotional eating and post-bariatric weight loss have focused overwhelmingly on female patients.

Research projects often result from the desire of such health practitioners to determine whether or not their theories or suspicions can be supported when subjected to the rigors of scientific investigation. We will assume that the research hypotheses for the examples and exercises have already been considered. Hypothesis Testing Steps For convenience, hypothesis testing will be presented as a ten-step procedure. It merely breaks the process down into a logical sequence of actions and decisions. The nature of the data that form the basis of the testing procedures must be understood, since this determines the particular test to be employed. Whether the data consist of counts or measurements, for example, must be determined. As we learned in the chapter on estimation, different assumptions lead to modifications of confidence intervals. The same is true in hypothesis testing: A general procedure is modified depending on the assumptions. In fact, the same assumptions that are of importance in estimation are important in hypothesis testing. We have seen that these include assumptions about the normality of the population distribution, equality of variances, and independence of samples. There are two statistical hypotheses involved in hypothesis testing, and these should be stated explicitly. The null hypothesis is sometimes referred to as a hypothesis of no difference, since it is a statement of agreement with (or no difference from) conditions presumed to be true in the population of interest. In general, the null hypothesis is set up for the express purpose of being discredited. Consequently, the complement of the conclusion that the researcher is seeking to reach becomes the statement of the null hypothesis. If the null hypothesis is not rejected, we will say that the data on which the test is based do not provide sufficient evidence to cause rejection. If the testing procedure leads to rejection, we will say that the data at hand are not compatible with the null hypothesis, but are supportive of some other hypothesis. The alternative hypothesis is a statement of what we will believe is true if our sample data cause us to reject the null hypothesis. Usually the alternative hypothesis and the research hypothesis are the same, and in fact the two terms are used interchangeably. Rules for Stating Statistical Hypotheses When hypotheses are of the type considered in this chapter an indication of equality рeither ј;; or! The null hypothesis is H 0: m ј 50 and the alternative is H A: m 6ј 50 Suppose we want to know if we can conclude that the population mean is greater than 50. Our hypotheses are H 0: m 50 H A: m > 50 If we want to know if we can conclude that the population mean is less than 50, the hypotheses are H 0: m! That is, the two together exhaust all possibilities regarding the value that the hypothesized parameter can assume. A Precaution It should be pointed out that neither hypothesis testing nor statistical inference, in general, leads to the proof of a hypothesis; it merely indicates whether the hypothesis is supported or is not supported by the available data. When we fail to reject a null hypothesis, therefore, we do not say that it is true, but that it may be true. When we speak of accepting a null hypothesis, we have this limitation in mind and do not wish to convey the idea that accepting implies proof. The test statistic is some statistic that may be computed from the data of the sample. As a rule, there are many possible values that the test statistic may assume, the particular value observed depending on the particular sample drawn. As we will see, the test statistic serves as a decision maker, since the decision to reject or not to reject the null hypothesis depends on the magnitude of the test statistic. General Formula for Test Statistic the following is a general formula for a test statistic that will be applicable in many of the hypothesis tests discussed in this book: test statistic ј relevant statistic А hypothesized parameter standard error of the relevant statistic pffiffiffi In Equation 7. It has been pointed out that the key to statistical inference is the sampling distribution. We are reminded of this again when it becomes necessary to specify the probability distribution of the test statistic.

Effectiveness of chlorhexidine bathing to reduce catheter-associated bloodstream infections in medical intensive care unit patients. Role of healthcare workers in outbreaks of methicillin-resistant Staphylococcus aureus: a 10-year evaluation from a Dutch university hospital. Controlling methicillin-resistant Staphylococcus aureus: quantifying the effects of interventions and rapid diagnostic testing. The impact of methicillin resistance in Staphylococcus aureus bacteremia on patient outcomes: mortality, length of stay, and hospital charges. Comparison of mortality associated with methicillin-resistant and methicillin-susceptible Staphylococcus aureus bacteremia: a meta-analysis. An outbreak of methicillin resistant Staphylococcus aureus on a burn unit: potential role of contaminated hydrotherapy equipment. Evaluation of a strategy of screening multiple anatomical sites for methicillin-resistant Staphylococcus aureus at admission to a teaching hospital. Methicillin-resistant Staphylococcus aureus infection or colonization present at hospital admission: multivariable risk factor screening to increase efficiency of surveillance culturing. Universal screening for methicillinresistant Staphylococcus aureus at hospital admission and nosocomial infection in surgical patients. Reduction of Staphylococcus aureus nasal carriage and infection in dialysis patients. Risk of methicillin-resistant Staphylococcus aureus infection after previous infection or colonization. Improving methicillin-resistant Staphylococcus aureus surveillance and reporting in intensive care units. Impact of routine intensive care unit surveillance cultures and resultant barrier precautions on hospital-wide methicillinresistant Staphylococcus aureus bacteremia. Identification of methicillin-resistant Staphylococcus aureus carriage in less than 1 hour during a hospital surveillance program. Impact of rapid screening tests on acquisition of meticillin resistant Staphylococcus aureus: cluster randomized crossover trial. Invasive methicillin-resistant Staphylococcus aureus infections in the United States. Reduction of surgical-site infections in cardiothoracic surgery by elimination of nasal carriage of Staphylococcus aureus. Distribution of multi-resistant Gram-negative versus Gram-positive bacteria in the hospital inanimate environment. Prevalence and risk factors for carriage of methicillin-resistant Staphylococcus aureus at admission to the intensive care unit. Successful long-term program for controlling methicillin-resistant Staphylococcus aureus in intensive care units. The role of non-critical health-care tools in the transmission of nosocomial infections. Routine screening for methicillin-resistant Staphylococcus aureus among patients newly admitted to an acute rehabilitation unit. Community-associated methicillin-resistant Staphylococcus aureus isolates causing healthcare-associated infection. A prolonged outbreak of methicillin-resistant Staphylococcus aureus in the burn unit of a tertiary medical center. Outbreak of invasive disease caused by methicillin-resistant Staphylococcus aureus in neonates and prevalence in the neonatal intensive care unit. Contamination of room door handles by methicillinsensitive/methicillin-resistant Staphylococcus aureus. Development and evaluation of a chromogenic agar medium for methicillin-resistant Staphylococcus aureus. Selective use of intranasal mupirocin and chlorhexidine bathing and the incidence of methicillin-resistant Staphylococcus aureus colonization and infection among intensive care unit patients. Universal surveillance for methicillin-resistant Staphylococcus aureus in 3 affiliated hospitals. Qualitative and (semi)quantitative characterization of nasal and skin methicillin-resistant Staphylococcus aureus carriage of hospitalized patients. Optimal surveillance culture sites for detection of methicillin-resistant Staphylococcus aureus in newborns.

We may determine the probability of observing x or fewer minus signs when given a sample of size n and parameter p by evaluating the following expression: Pрk x j n; pЮ ј x X kј0 n Ck p k nАk q (13. In Appendix Table B we find P рk 1j9;:5Ю ј:0195 With a two-sided test either a sufficiently small number of minuses or a sufficiently small number of pluses would cause rejection of the null hypothesis. Since, in our example, there are fewer minuses, we focus our attention on minuses rather than pluses. An alternative way of stating the null hypothesis is PрX i > Y i Ю ј PрX i < Y i Ю ј:5 One of the matched scores, say, Yi, is subtracted from the other score, Xi. If Yi is less than Xi, the sign of the difference is ю, and if Yi is greater than Xi, the sign of the difference is А. If the median difference is 0, we would expect a pair picked at random to be just as likely to yield a ю as a А when the subtraction is performed. By means of the sign test, we can decide how many of one sign constitutes more than can be accounted for by chance alone. Twelve pairs of patients seen in a dental clinic were obtained by carefully matching on such factors as age, sex, intelligence, and initial oral hygiene scores. One member of each pair received instruction on how to brush his or her teeth and on other oral hygiene matters. Six months later all 24 subjects were examined and assigned an oral hygiene score by a dental hygienist unaware of which subjects had received the instruction. We assume that the population of differences between pairs of scores is a continuous variable. If the instruction produces a beneficial effect, this fact would be reflected in the scores assigned to the members of each pair. If, in fact, instruction is beneficial, the median of the hypothetical population of all such differences would be less than 0, that is, negative. If, on the other hand, instruction has no effect, the median of this population would be zero. The sampling distribution of k is the binomial distribution with parameters n and. As will be seen, the procedure here is identical to the single sample procedure once the score differences have been obtained for each pair. Performing the subtractions and observing signs yields the results shown in Table 13. The nature of the hypothesis indicates a one-sided test so that all of a ј:05 is associated with the rejection region, which consists of all values of k (where k is equal to the number of ю signs) for which the probability of obtaining that many or fewer pluses due to chance alone when H0 is true is equal to or less than. When we eliminate the zero, the effective sample size is n ј 11 with two pluses and nine minuses. In other words, since a "small" number of plus signs will cause rejection of the null hypothesis, the value of our test statistic is k ј 2. We want to know the probability of obtaining no more than two pluses out of 11 tries when the null hypothesis is true. As we have seen, the answer is obtained by evaluating the appropriate binomial expression. In this example we find P рk 2 j11;:5Ю ј 2 X kј0 11 C k р:5Ю k р:5Ю11Аk By consulting Appendix Table B, we find this probability to be. We have also seen that the alternative hypothesis may lead to either a one-sided or a two-sided test. In either case we concentrate on the less frequently occurring sign and calculate the probability of obtaining that few or fewer of that sign. We use the least frequently occurring sign as our test statistic because the binomial probabilities in Appendix Table B are "less than or equal to" probabilities. By using the least frequently occurring sign, we can obtain the probability we need directly from Table B without having to do any subtracting. If the probabilities in Table B were "greater than or equal to" probabilities, which are often found in tables of the binomial distribution, we would use the more frequently occurring sign as our test statistic in order to take advantage of the convenience of obtaining the desired probability directly from the table without having to do any subtracting. In fact, we could, in our present examples, use the more frequently occurring sign as our test statistic, but because Table B contains "less than or equal to" probabilities we would have to perform a subtraction operation to obtain the desired probability. If we use as our test statistic the most frequently occurring sign, it is 9, the number of minuses. The desired probability, then, is the probability of nine or more minuses, when n ј 11 and p ј:5.

This quantity, referred to as the sum of squares of the residuals, may also be written as XА X Б2 yj А ^j y (10. This method of obtaining the estimates is tedious, time-consuming, subject to errors, and a waste of time when a computer is available. Those interested in examining or using the arithmetic approach may consult earlier editions of this text or those by Snedecor and Cochran (1) and Steel and Torrie (2), who give numerical examples for four variables, and Anderson and Bancroft (3), who illustrate the calculations involved when there are five variables. Prior to analyzing the data using multiple regression techniques, it is useful to construct plots of the relationships among the variables. This is accomplished by making separate plots of each pair of variables, (X1, X2), (X1, Y), and (X2, Y). We see from the output that the sample multiple regression equation, in the notation of Section 10. Additional information on the score made by each nurse on an aptitude test, taken at the time of entering nursing school, was made available to the researcher. The complete data are as follows: State Board Score (Y) 440 480 535 460 525 480 510 530 545 600 495 545 575 525 575 600 490 510 575 540 595 525 545 600 625 Total 13, 425 Final Score (X1) 87 87 87 88 88 89 89 89 89 89 90 90 90 91 91 91 92 92 92 93 93 94 94 94 94 2263 Aptitude Test Score (X2) 92 79 99 91 84 71 78 78 71 76 89 90 73 71 81 84 70 85 71 76 90 94 94 93 73 2053 10. The variables are Y X1 X2 X3 X4 X5 X6 Patient 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ј ј ј ј ј ј ј mean arterial blood pressureрmm HgЮ ageрyearsЮ weightрkgЮ body surface areaрsq mЮ duration of hypertensionрyearsЮ basal pulseрbeatsthn=minЮ measure of stress Y 105 115 116 117 112 121 121 110 110 114 114 115 114 106 125 114 106 113 110 122 X1 47 49 49 50 51 48 49 47 49 48 47 49 50 45 52 46 46 46 48 56 X2 85. In our study of simple linear regression we have learned that the usefulness of a regression equation may be evaluated by a consideration of the sample coefficient of determination and estimated slope. In evaluating a multiple regression equation we focus our attention on the coefficient of multiple determination and the partial regression coefficients. The Coefficient of Multiple Determination In Chapter 9 the coefficient of determination is discussed in considerable detail. The total variation present in the Y values may be partitioned into two components-the explained variation, which measures the amount of the total variation that is explained by the fitted regression surface, and the unexplained variation, which is that part of the total variation not explained by fitting the regression surface. The unexplained Б2 P y variation, written as yj А ^j, is the sum of squared deviations of the original observations from the calculated values. Testing the Regression Hypothesis To determine whether the overall regression is significant (that is, to determine whether R2 is significant), we may y:12 perform a hypothesis test as follows. The research situation and the data generated by the research are examined to determine if multiple regression is an appropriate technique for analysis. We assume that the multiple regression model and its underlying assumptions as presented in Section 10. In words, the null hypothesis states that all the independent variables are of no value in explaining the variation in the Y values. If we reject H0 we conclude that, in the population from which the sample was drawn, the dependent variable is linearly related to the independent variables as a group. If we fail to reject H0, we conclude that, in the population from which our sample was drawn, there may be no linear relationship between the dependent variable and the independent variables as a group. If H0 is true and the assumptions are met, the test statistic is distributed as F with 2 numerator and 68 denominator degrees of freedom. We conclude that, in the population from which the sample came, there is a linear relationship among the three variables. Inferences Regarding Individual b0 s Frequently, we wish to evaluate the strength of the linear relationship between Y and the independent variables individually. That is, we may want to test the null hypothesis that bi ј 0 against the alternative bi 6ј 0рi ј 1; 2;. The validity of this procedure rests on the assumptions stated earlier: that for each combination of Xi values there is a normally distributed subpopulation of Y values with variance s 2. Hypothesis Tests for the bi To test the null hypothesis that bi is equal to some particular value, say, bi0, the following t statistic may be computed: tј ^ bi А bi0 sbi ^ (10. The null hypothesis is rejected since the computed value of t, А3:80, is less than А1:9957. For this test, p < 2р:005Ю ј:01 because А3:80 < А2:6505 (obtained by interpolation). Confidence Intervals for the bi When the researcher has been led to conclude that a partial regression coefficient is not 0, he or she may be interested in obtaining a confidence interval for this bi. Confidence intervals for the bi may be constructed in the usual way by using a value from the t distribution for the reliability factor and standard errors given above.