Neurons in the cortex are characterized by irregular spiking patterns that can be correlated across the population. However, both the variability and covariability in neuronal activity can be modulated by stimuli (Churchland et al., 2010). The reduction in variability and covariability observed experimentally has been explained using multi-attractor models (Ponce-Alvarez et al., 2013), and chaotic networks (Molgedey et al., 1992). In this paper the authors propose an alternative explanation using a stochastic, stabilized supralinear network (SSN). The main mechanism driving the modulation in this model is stabilizing inhibitory feedback.
In multi-attractor models, the network operates in a multi-stable regime and in the absence of stimulus fluctuations causes the network to wander between different attractors. This meandering gives rise to correlated variability in the activity of different cells. Upon stimulus onset, the variability is suppressed as the network’s activity is pinned to the neighborhood of a single attractor. In chaotic models, variability is due to chaotic fluctuations in activity. Certain types of stimuli can suppress such chaotic fluctuations by forcing network dynamics to follow specific trajectories, thus quenching variability across trials. While both of these models explain stimulus-induced reduction of variability, only the multi-attractor models can explain the stimulus-tuning of variability reduction. Even then, this requires either considerable parameter tuning or very strong noise.
To address this question the authors present an alternative way to explain this phenomenon using a stochastic stabilized supralinear network (SSN). The dynamics of the spiking SSN is defined via equations governing the voltages of the individual neurons:
Neurons integrate their external and recurrent inputs linearly in their membrane potential, but their output (rate) is a nonlinear function of the voltage. The quantity  is noise, and
is noise, and 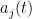 is the low pass filtered version of the spike train of neuron
is the low pass filtered version of the spike train of neuron 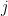 . Neuron
. Neuron 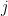 generates spikes at each time bin
generates spikes at each time bin 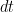 with an instantaneous probability
with an instantaneous probability 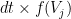 , where
, where 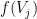 is the instantaneous firing rate of that neuron.
is the instantaneous firing rate of that neuron.
The choice of the nonlinearity, 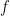 , translating voltage into spikes is the crucial part of the model. As shown in earlier work by the authors (Ahmadian et al, 2013), this function needs to be superlinear, and here a threshold-quadratic function is chosen. To understand the mechanics of variability modulation SSNs the authors linearize the dynamics around the input dependent fixed point, and obtain a Schur decomposition of the Jacobian matrix. This allows them to show analytically that transient variability increases for weak inputs, due to weak recurrent inhibitory self coupling and strong balance amplification. Variability decreases for strong inputs due to the supralinear growth in recurrent inhibition, stabilizing the fixed point and damping fluctuations. This mechanism can already be understood using a network of two units representing the excitatory (E) and inhibitory (I) subpopulations, respectively: Weak inputs lead to an increase in variability (across trials). However, for strong inputs variability is suppressed. Modulation in variability requires recurrent interactions: a feed-forward circuit is not enough.
, translating voltage into spikes is the crucial part of the model. As shown in earlier work by the authors (Ahmadian et al, 2013), this function needs to be superlinear, and here a threshold-quadratic function is chosen. To understand the mechanics of variability modulation SSNs the authors linearize the dynamics around the input dependent fixed point, and obtain a Schur decomposition of the Jacobian matrix. This allows them to show analytically that transient variability increases for weak inputs, due to weak recurrent inhibitory self coupling and strong balance amplification. Variability decreases for strong inputs due to the supralinear growth in recurrent inhibition, stabilizing the fixed point and damping fluctuations. This mechanism can already be understood using a network of two units representing the excitatory (E) and inhibitory (I) subpopulations, respectively: Weak inputs lead to an increase in variability (across trials). However, for strong inputs variability is suppressed. Modulation in variability requires recurrent interactions: a feed-forward circuit is not enough.
The insights obtained from analyzing a two population model hold more generally. The authors next considered a network of 5,000 neurons (80% E and 20% I) randomly connected with low probability and synaptic weights chosen from the population model (meaning any two neurons from populations  and
and 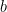 connected with the same strength, for
connected with the same strength, for 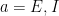 and
and  ). In this case, variability suppression was achieved at the single cell level (voltage), as well as at the population level (LFP and rates). This model primarily suppressed shared rather than private variability, which was also observed in experiments (Churchland et al, 2010). This is due to effective mean field connectivity in the network causing the dynamics to be coupled to network-wide patterns of activity across
). In this case, variability suppression was achieved at the single cell level (voltage), as well as at the population level (LFP and rates). This model primarily suppressed shared rather than private variability, which was also observed in experiments (Churchland et al, 2010). This is due to effective mean field connectivity in the network causing the dynamics to be coupled to network-wide patterns of activity across  or across
or across  cells. These patterns were affected by the changes in effective connectivity due to the stimulus. Significant variability in these patterns was present due to correlated noise. Hence, shared
cells. These patterns were affected by the changes in effective connectivity due to the stimulus. Significant variability in these patterns was present due to correlated noise. Hence, shared  and
and  patterns behaved as units from the population model, and variability suppression also caused suppression of covariability. In addition, the model accounts for the stimulus-induced modulation of the power spectrum and cross-coherence of LFP and single cell voltage seen experimentally in visual area V1 of awake monkeys.
patterns behaved as units from the population model, and variability suppression also caused suppression of covariability. In addition, the model accounts for the stimulus-induced modulation of the power spectrum and cross-coherence of LFP and single cell voltage seen experimentally in visual area V1 of awake monkeys.
Since in this model the network was randomly connected, and neurons were not stimulus selective, variability was suppressed uniformly across the population. However, experiments show that variability suppression depends on stimulus tuning. Therefore, the authors next introduced an extension of the network with a ring architecture, with neurons around the ring having different preferred orientations (PO). In accord with previous models of this type (Ponce-Alvarez et al., 2013; Lombardo et al., 2015; Lin et al., 2015), neurons with similar tuning were connected more strongly than neurons with large difference in PO. In this network, a bump of activity is present only when a stimulus is present, and does not represent the short term memory of the stimulus. The dynamics of this model agree well with data from V1 in awake monkeys: The model displays variability suppression at the single cell level and at the population level, a drop in the Fano factor, and U-shaped tuning of variability suppression with stimulus orientation in Fano factors and membrane potentials. In particular, the fact that shared variability was mainly suppressed over private variability is due to the spatially smooth connectivity profile, resulting in regular patterns of activity across the population.
The authors examined the structure of quenched noise variability after stimulus onset. They showed that most of the shared variability arose from variability in the location and width of the bump of activity. These small transformations resulted in a characteristic pattern of deviation of network activity from the mean bump. These two patterns contributed two distinct spatial covariance templates, which taken together accounted for 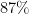 of the structure in the full covariance matrix of the network. Hence, bump kinetics correctly predicted membrane potential variances.
of the structure in the full covariance matrix of the network. Hence, bump kinetics correctly predicted membrane potential variances.
As mentioned before, chaotic models cannot account for stimulus-modulated changes in variability, because neurons are not tuned to different stimuli. Therefore, the authors compared the SSN to the multi-attractor model, in order to determine if their proposed mechanism better explains the suppression in variability seen in experiments. They find that multi-attractor networks show a more limited repertoire of variability patterns. In the SSN model fluctuations in bump location and width led to very weak variability modulation between orthogonal cells, and a much shallower modulation between similarly tuned cells. The attractor model did not display this cancellation even for orthogonally tuned cells. Therefore, correlations between orthogonally tuned cells were modulated as strongly as similarly tuned cells, in disagreement with experimental data.
Lastly, the authors explored the temporal dynamics of variability modulation, because this can potentially show fundamental differences between the three different mechanisms. In order to do so, they measured the timescales on which suppression and recovery of variability took place. For SSNs, suppression and recovery was fastest and in the same timescale as the membrane time constant, in agreement with experiments. In contrast, chaotic networks were 4-15 times slower, and the multi-attractor network was at least 20 times slower than the single cell time constant.
In conclusion, the authors proposed a robust model (SSN) which can capture key aspects of variability modulation, such as stimulus-induced quenching, stimulus-tuned quenching, and realistic timescales of suppression and recovery, without the need of precise fine-tuning of parameters, or large amounts of noise. The main insight here is that in SSNs, the supra linear dependence of firing on inputs increases the effective connectivity with increasing input, which in turn modulates the variability and covariability of responses. Two remarkable effects that explain modulation of variability: balanced amplification, which amplifies variability due to E-I interactions and dominates at weak input; and inhibitory feedback, which quenches variability by generating strong inhibitory input in the network and dominates at large inputs. In combination, these mechanisms robustly reproduce experimentally observed spatial and temporal patterns of variability quenching and modulation.
References:
[1] Ahmadian, Y., Rubin D.B., and Miller K.D. (2013). Neural Comput. 25, 1994-2037.
[2] Churchland, M.M., Yu, B.M., Cunningham, J.P., Sugrue, L.P., Cohen, M.R., Corrado, G.S., Newsome, W.T., Clark, A.M., Hosseini, P., Scott, B.B., et al. (2010). Nat. Neurosci. 13, 369-378.
[3] Lin, I.-C., Okun, M., Carandini, M., and Harris, K.D. (2015). Neuron 87, 644-656.
[4] Lombardo, J., Macelliao, M., Liu, B., Osborne, L.C., and Palmer, S.E. (2015). In 2015 Neuroscience Meeting Planner (online) (Washington, DC: Society for Neuroscience).
[5] Molgedey, L., Schuchhardt, J., and Schuster, H.G. (1992). Phys. Rev. Lett. 69, 3717-3719.
[6] Ponce-Alvarez, A., Thiele, A., Albright, T.D., Stoner, G.R., and DEco, G. (2013). Proc. Natl. Acad. Sci. USA 110, 13162-13167.