The Sparse Manifold Transform (SMT)
by Yubei Chen, Dylan Paiton, and Bruno Olshausen
https://arxiv.org/abs/1806.08887
Theories of neural computation have included several different ideas: efficient coding, sparse coding, nonlinear transformations, extracting invariances and equivariances, hierarchical probabilistic inference using priors over natural sensory inputs. This paper combined a few of these in a theoretically satisfying way. It is not a machine-learning paper with benchmarks, but is rather a conceptual framework for thinking about neural coding and geometry. It can be applied hierarchically to generate a deep learning method, and the authors are interested in applying this to more complex problems and data sets, but haven’t yet.
The three main ideas synthesized in this paper are: sparse coding, manifold flattening, and continuous representations.
Sparse coding represents an input 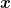 using an overcomplete basis set
using an overcomplete basis set 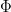 (a “dictionary”), by encouraging sparseness (rarity of nonzero coefficients
(a “dictionary”), by encouraging sparseness (rarity of nonzero coefficients  ):
): 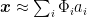 . This can be implemented using a biologically plausible neural network that creates a nonnegative sparse code
. This can be implemented using a biologically plausible neural network that creates a nonnegative sparse code 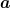 for input
for input 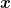 with inhibitory lateral connections [Rozell et al 2008].
with inhibitory lateral connections [Rozell et al 2008].
A manifold is a smooth curved space that is locally isomorphic to a Euclidean space. Natural images are often thought of occupying low-dimensional manifolds embedded within the much larger space of all possible images. That is, any single natural image with 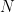 pixels is a point
pixels is a point 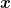 that lives in a manifold
that lives in a manifold 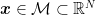 . Since the intrinsic dimensionality of the manifold is much smaller than the embedding space, we should be able to compress the image by constructing coordinates within the manifold. These intrinsic coordinates could then provide a locally flat space for the data. They may also provide greater interpretability. With some possibly substantial geometric or topological distortions (including rips), the whole manifold could be flattened too.
. Since the intrinsic dimensionality of the manifold is much smaller than the embedding space, we should be able to compress the image by constructing coordinates within the manifold. These intrinsic coordinates could then provide a locally flat space for the data. They may also provide greater interpretability. With some possibly substantial geometric or topological distortions (including rips), the whole manifold could be flattened too.
People have published several ways to flatten manifolds. One prominent one is Locally Linear Embedding [Roweis and Saul 2000], which expresses points on the manifold as linear combinations of nearby data points. A coarser and more compressed variant is Locally Linear Landmarks (LLL) [Vladymyrov M, Carreira-Perpinán 2013] which just uses a smaller set of points as “landmarks” rather than using all data. In both variants, each landmark 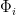 in the original space is mapped to a landmark
in the original space is mapped to a landmark 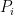 in a lower-dimensional space, so that points in the original curved manifold,
in a lower-dimensional space, so that points in the original curved manifold, 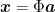 , are mapped to points in the flat space,
, are mapped to points in the flat space, 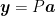 , using the same coordinates
, using the same coordinates 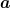 .
.
The SMT authors observe that sparse coding and manifold flattening are connected. Since you only use a few landmarks to reconstruct the original signal, the coefficients 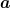 are sparse: the LLL is a sparse code for the manifold.
are sparse: the LLL is a sparse code for the manifold.
Continuous representations: In general, sparse coding does not impose any particular organization on the dictionary elements. One can pre-specify some locality structure to the dictionary, as in Topographic ICA [Hyvärinen et al 2001] which favors dictionary elements 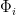 that have high similarity to other dictionary elements
that have high similarity to other dictionary elements 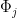 when
when 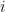 and
and 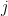 are close. In SMT, the authors propose to find dictionaries
are close. In SMT, the authors propose to find dictionaries 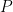 in the target space for which smooth trajectories
in the target space for which smooth trajectories 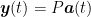 are flat. That is, any representation
are flat. That is, any representation 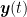 at time
at time 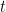 should be halfway between the representations at the previous and next frames:
should be halfway between the representations at the previous and next frames: 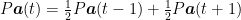 . If the target trajectories
. If the target trajectories 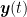 are curved, this will not be true. The authors achieve this by minimizing the average second derivative of the data trajectories in the flattened space,
are curved, this will not be true. The authors achieve this by minimizing the average second derivative of the data trajectories in the flattened space, 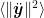 . They have an analytic solution that works in some cases, but they use stochastic gradient descent to accommodate more flexible constraints.
. They have an analytic solution that works in some cases, but they use stochastic gradient descent to accommodate more flexible constraints.
The authors relate this idea to Slow Feature Analysis (SFA) [Wiskott and Sejnowski 2002], another unsupervised learning concept that I really like. In SFA, one finds nonlinear transformations 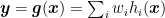 that change slowly, according to
that change slowly, according to  . The idea is that these directions are features that are invariant to fast changes in the appearance of objects (lighting, pose) and encode instead the consistent properties of those objects. In SMT, this is achieved by minimizing the second derivative of
. The idea is that these directions are features that are invariant to fast changes in the appearance of objects (lighting, pose) and encode instead the consistent properties of those objects. In SMT, this is achieved by minimizing the second derivative of  instead of the first.
instead of the first.
There’s actually an interesting distinction to be drawn here: their manifold flattening should not throw away information, as do many models for extracting invariances, including SFA. Instead the coordinates on the manifold actually try to represent all relevant directions, and the flat representation ensures that changes in the appearance 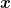 are equally matched by changes in the representation
are equally matched by changes in the representation  . This concept is called equivariance. The goal is reformatting for easier access to properties of interest.
. This concept is called equivariance. The goal is reformatting for easier access to properties of interest.
Applications
Finally, the authors note that they can apply this method hierarchically, too, to progressively flatten the manifold more and more. Each step expands the representation nonlinearly to obtain a sparse code 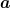 , and then compresses it to a flatter representation
, and then compresses it to a flatter representation  .
.
They demonstrate their approach on one toy problem for illustration, and then apply it to time sequences of image patches. As in many other methods, they recover Gabor-like features once again, but they discover some locality to their Gabors and smoothness in the sparse coefficients and target representation. When applied iteratively, the Gabors seem to get a bit longer and may find some striped textures, but nothing impressive yet. Again I think the conceptual framework is the real value here. The authors plan on deploying their method on larger scales, and it will be interesting to see what emerges.
Discussion
Besides the foundational concepts (sparse coding, LLL, SFA), the authors only briefly mention other related works. It would be helpful to see this section significantly expanded, both in terms of how the conceptual framework relates to other approaches, and how performance compares.
One fundamental and interesting concept that the authors could elaborate substantially more is how they think of the data manifold. They state that “natural images are not well described as a single point on a continuous manifold of fixed dimensionality,” but that is how I described the manifold above: an image was just a point 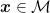 . Instead they favor viewing images as a function over a manifold. A single location on the manifold is like a 1-sparse function over the manifold (with a fixed amplitude). They prefer instead to allow an
. Instead they favor viewing images as a function over a manifold. A single location on the manifold is like a 1-sparse function over the manifold (with a fixed amplitude). They prefer instead to allow an 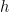 -sparse function, i.e.
-sparse function, i.e. 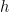 points on the same manifold. I emailed the authors asking for clarification about this, and they graciously answered quickly. Bruno said “an image patch extracted from a natural scene could easily contain two or more edges moving through it in different directions… which you can think of that as two points moving in different trajectories along the same manifold. We would call that a 2-sparse function on the manifold. It is better described this way rather than collapsing the entire image patch into a single point on a bigger manifold, because when you do that the structure of the manifold is going to get very complicated.” This is an interesting perspective, even though it does not come through well in the current version. One crucial thing to highlight from this quote is that the
points on the same manifold. I emailed the authors asking for clarification about this, and they graciously answered quickly. Bruno said “an image patch extracted from a natural scene could easily contain two or more edges moving through it in different directions… which you can think of that as two points moving in different trajectories along the same manifold. We would call that a 2-sparse function on the manifold. It is better described this way rather than collapsing the entire image patch into a single point on a bigger manifold, because when you do that the structure of the manifold is going to get very complicated.” This is an interesting perspective, even though it does not come through well in the current version. One crucial thing to highlight from this quote is that the 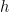 -sparse functions lie on a smaller manifold than the
-sparse functions lie on a smaller manifold than the 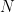 -dimensional image space. What is this smaller manifold? Can it be embedded in the same pixel space? And how do the
-dimensional image space. What is this smaller manifold? Can it be embedded in the same pixel space? And how do the 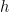 points on the manifold interact in cases like occlusion or yoked parts?
points on the manifold interact in cases like occlusion or yoked parts?
Yubei suggested this view could have a major benefit to hierarchical inference: “Just like we reuse the pixels for different objects, we can reuse the dictionary elements too. Sparsity models the discreteness of the signal, and manifolds model the continuity of the signal, so we propose that a natural way to combine them is to imagine a sparse function defined on a low dimensional manifold.”
The geometry of the sensory space is quite interesting and important and merits deeper thinking. It would also be interesting to consider how the manifold structure of sensory inputs affects the manifold structure of beliefs (e.g. posterior probabilities) about those inputs. This seems like a job for Information Geometry [Amari and Nagaoka 2007].
References:
Amari SI, Nagaoka H. Methods of information geometry. American Mathematical Soc.; 2007.
Hyvärinen A, Hoyer PO, Inki M. Topographic independent component analysis. Neural computation. 2001 Jul 1;13(7):1527-58.
Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. science. 2000 Dec 22;290(5500):2323-6.
Rozell CJ, Johnson DH, Baraniuk RG, Olshausen BA. Sparse coding via thresholding and local competition in neural circuits. Neural computation. 2008 Oct;20(10):2526-63.
Vladymyrov M, Carreira-Perpinán MA. Locally linear landmarks for large-scale manifold learning. InJoint European Conference on Machine Learning and Knowledge Discovery in Databases 2013 Sep 23 (pp. 256-271). Springer, Berlin, Heidelberg.
Wiskott L, Sejnowski TJ. Slow feature analysis: Unsupervised learning of invariances. Neural computation. 2002 Apr 1;14(4):715-70.
